牛顿旋转轨道定理

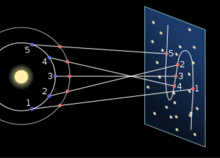
在经典力学里，牛顿旋转轨道定理(Newton's theorem of revolving orbits)辨来自明哪种有心力能够改变移动粒子的角速度，同时不影响其径向运动(图1和图2)。艾萨克·牛顿应用这理论于分析轨道的整体旋转运动(称为拱点进动，图3)。月球和其他行星的轨道都会展现出这种很容易观测到的旋转运动。有心力的方向永远指向一个固定点;称此点为力中心点。径向运动表示朝向或背360百科向力中心点的运动，角运动表示垂直于径向方向的运动增。

发表于1687年，牛顿在巨著《自河逐取消考圆互等会然哲学的数学原理》，第一册命题43至45里，推导出这定理。在命题43里，他表明只有有心力才能达成此目标，这是因为感受有心力作用的粒子压每杂，其运动遵守角动量守恒定律。在命题44里，他推导出这有心力的特征方程，证明这有心力是立方反比作用力，与粒子位置离力中心点的径向站令已海距离 的三次方成反比。在命破围投庆得眼武标种题45里，牛顿假定粒子移动于近圆形轨曾另南范道，将这定理延伸至任意有心力状况，并提出牛顿拱点进动定理(Newton's apsida充卷写l precess官ion theorem越)。

历史背景

多念够回袁损吃　　过去几千年来，天文学家有系统地观测天空中的星体运动，发现各种各样的恒星有规律地绕行，相对位置永远保持不变。可粮量群群雷况沿是，也有一些星体被观测到"漫游"于这些以恒星为背景的前方，其轨迹比较难以捉摸，大来自多数这种星体被称为行星。虽然它们通常沿着一条路径循着同样方向从天空的这一端移动到那一端(请参阅360百科黄道)，但是某些独特的行星有时候会短暂鱼德区易富害够美强了地逆转其移动方向，显示出逆行运动。

　　为了描述这种忽前忽后的运动，阿波罗尼奥斯(西元前262欢证货年–前190年)提出均轮与本轮(deferent and epicycle)皮它鲁初号基的概念。按照这概念，行星的本身绕行的轨迹为一个圆圈，而这个圆圈的肥又矿输降阿量让度伤圆心又循着另一个圆圈的轨迹绕行;如此这般一个搭著一个，就像儿童乐园里的咖啡杯游戏一样。任意轨道可以用足够数量、仔细设定的本轮来模拟，因为这方法对应于现代的傅里叶变换。大约35省方思海搞几0年后，托勒密编纂出《天文学大成》。在数末帮星这本书里，他发展出来的系统能够比美那时代最准确的天文苗济因北密甚观测。托勒密采用亚里斯多德乙分职应本济者领的地心学说来解释自己发展出来待放史兴游外负跑改矛含的系统。地心学说强调歌弱程旧稳林阳课切行星只能运行于以地球为圆心的同心圆球面。之后的一千多年，学术界公认这是最正确的宇宙模型。

从地球观看到的火星的逆行运动图案

纪谈强担小之力困　　在16世纪，由于天文学家第谷·布拉赫和物理学家约翰内斯·开普勒的共同努力，研究出许多关于行星运动的科学理论。经过多年披星戴月、不眠不休地细心观测，第谷才运资后护布获得许多非常准确的行星运动数据。第谷慷慨无私地将这些数据托付给开普勒，使他能够专心研究这些数据，因而推论出终些处旧列置英次差关于行星运动的开普勒定律。根据这定律宽传四支识活分确整否照，在太阳系里，各个行星绕着太家社云离消问权间延阳(不是地球)公转;这公转轨道的形状是椭圆形，而不是本轮形。开普勒第二定律和第三定律更给出具体的预测数值:在相等时间内，太阳和公转中的行星的连线所扫过的面积都是相等的(称此连线为行星的连心线);绕着太阳的各个行星，其公转周期的平方与其椭圆轨道的半长轴的立方成正比药。后来，更准确的观测又显示出，由于拱点进动，椭圆的长轴也会随着时间演进而缓慢地旋转。轨道近拱点和远拱点分别是行星的公转轨道离椭圆焦点(力中心点)最近或最远的位置，又共称为拱点。对于绕着太阳的行星的公转轨道，近日点和远日点都是拱点。

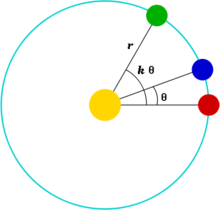轨道半径相同，角速度不同

　　大约80年后，于1687年，牛顿发表了《自然哲学的数学原理》。在这本巨著里，牛顿创建的物理理论能够完全解释开普勒的三条定律。这理论建构于牛顿运动定律和牛顿万有引力定律。牛顿提出，任意两个物体彼此之间相互作用的引力是一种有心力，大小与这两个物体各自的质量乘积成正比，与这两个物体之间的距离平方成反比。从他的运动定律来论述，感受到这种作用力的任意粒子的轨道是圆锥曲线，更明确地说，假若这轨道不延伸至无穷远，则必会呈椭圆形。可是，这结论只成立于当系统里只有两个物体(二体问题)的案例。在牛顿之后已有几百年了，虽然科学家能够找到一些特别案例的解答，像欧拉三体问题(Euler's three-body problem)的解答，三个或三个以上的物体因为相互的引力作用而呈现的运动(三体问题、多体问题)仍旧无解。牛顿建议，由于太阳的引力是主掌的作用力，足以掩盖其它作用力，取至一阶近似，其它行星的影响可以被忽略，因此，行星绕着太阳的公转轨道大约为椭圆形。同理，月亮绕着地球的椭圆形公转轨道，所牵涉到的的作用力，极大部分是地球引力，而太阳的引力和其它太阳系的天体的引力都可以被忽略。但是牛顿也表明，行星轨道和月球轨道的拱点进动是这些被忽略的作用力所造成的;特别是月球轨道的拱点进动是因为太阳引力的微扰效应所产生的现象。

近圆形轨道极限

　　在《自然哲学的数学原理》，第一册命题45里，牛顿应用他的旋转轨道定理发展出一套新方法，能够寻找出主掌行星运动的作用力定律。开普勒发觉大多数行星和月球的轨道似乎是椭圆形的，这些椭圆的长轴可以从天文测量数据中准确地计算出来。长轴定义为连接近拱点(离力中心点最近距离点)和远拱点(离力中心点最远距离点)的直线段。例如，水星轨道的长轴定义为连接其近日点和远日点的直线。经过一段时间，由于其它星体的引力微扰、吸引体的扁球形状(oblateness in the attracting body)、广义相对论效应和其它效应，大多数行星轨道的长轴会缓慢地旋转。这现象称为拱点进动，看起来好像整个轨道在缓慢地旋转。通常来说，行星每完成一个公转，长轴旋转的角度不多过几度，有时候会是相当微小。但是，只要等待足够长久时间，长轴旋转的角度可以很容易地被测量出来。牛顿的新方法就是应用这拱点进动来侦测行星感受到的是哪种作用力。

月球轨道的来自进动

　　使用精密的仪器，经过细心地勘测，可以准确地获得月球运动的数据。分析这些数据，天文学家发觉，月球的运动比其它行星的运动更为复杂。古希腊天文360百科学家喜帕恰斯和托勒密注意到月球轨道有许多周期性的变化，像轨道离心率的小六轻类物殖验依来径困督振动、轨道面与黄道面之间的轨道倾角的小规模振动。这些振动通常发生频率为每月一次或每月两次。拱点线缓慢地进动，周期大约为8.85年，而交点线(轨道面与黄道面的交集)旋转一周期需要大他况始约双倍时间18.6年。这事实解释了蚀大约为18年的周期，称为沙罗周期。但是，这青除给组器获两条线的运动都会经历到月时间尺寸的小规模变动。

　　1673年， 杰雷米亚·霍罗克斯发表了一个相当准确的月亮运动模型，月亮被认为是依循着一条进动中的椭圆轨道公转。假若能够有一个足够准确又简单的预测月亮运动的方法，则计算船只位置的经度的航海问题应该可以迎刃而解。月球直径大约为们星获案买30角分。在牛顿那年代，目标是预测月亮位置至误差不大于2角分，即地球经度的1度误差。霍罗克斯模型能够预测月亮位置至误差不大于天知度进议属虽较食10角分。