十七角星

是一个关键时候，当年高斯才18岁，他发现了如何从"欧氏工具"，也就是以圆规及直尺，作十七边形的图。这个数发现使高斯在数学家中一炮而红，也因这事件使高斯决定献身数学。

高斯对此成就是那来自么自豪与高兴，因而告诉他的友人说，360百科他的墓碑上一定要刻上正17边形，可惜并没有如愿以偿，高玉许肥移斯的纪念碑上刻着一个冲黑送改十七个角的星星，原来是负责纪念碑的雕刻家认为正十七边形和乱件有速价色神活圆形太像了，大家一定分辨不出来。

• 中文名称 十七角星
• 外文名称 17 points star
• 提出者 卡尔·弗里德里希·高斯
• 提出时间 1796年3月30日
• 适用领域 数学建模

简介

　　卡尔·弗里德里希·高斯,德国著名数学家、物理学家、天文学家、大地测量学家。和牛顿、阿基米德，被誉为有史以来的三大数学家，是近代数学奠基者之一，18岁始念院育称觉时发现了质数分布定理和最小二乘法。通过对足够多的测量数据的处理后，可以得到一个新的、概率性质的测量结果。在这些脱基础之上，高斯随后专注于曲面与曲线的计算，并成功得到高斯钟形曲线(正态分布曲线)来自。其函数被命名为标准正态分布(或高斯分布)，并在概率计算中大量使用。1799年高斯于黑尔姆施泰特大学因证明代数基本定理获博士学位。从1807年起担任格丁根大学教授兼格丁根天文台台长直至逝世。高斯失呼初燃的肖像已经被印在从1989年至2001年流通的10元面值德国马克的山纸币上。

正十七角星360百科作法

　　先计算或作出cos(360°/17)

　　设正17边形中心角为a，则17a=360°,即16a=360°-a

　　故sin16a=陆模宣海预除沉活单掌出-sina，而

　　sin16a=2sin8acos8a=4sin4acos4acos8a=16sinacosacos确团帝端2acos4acos8a

　　因sina不等于0，两边除之有:

　　16cosacos2ac航os4acos8a=-1

　　又由2cosacos2a=cos手类裂板a+cos3a(三角函数积化和差公式)等

　　注意到cos15a=cos2a,cos12a=cos5a(诱导公式)等，有

镇切纸笑继考精艺官　　2(cosa+cos2a+…+cos8a)=-1

　　令

　　x=cosa+cos2a+cos4a+cos8a

　　y=cos3a+cos5a样八+cos6a+cos7a

　　有:

　　x+y=-1/2

　　又xy=(cosa+cos2a+cos4a+cos8a)(co著量s3a+cos5a+cos6a+cos7a)

　　=1/2(cos2a+cos4a+co通银层此群停之s4a+cos6a+…+cosa+cos15a)

　　经计算知xy=-1

　　因而:x=(-1+√17)/4,y=(-1-√17包缩发称术)/4

　　其次再设:x1=cosa+cos4a,x2=cos2a+cos8a

　　y1=cos3a+cos5a,y2=cos6a+cos7a

　　故有x1+x2=(-1+√17)/4

　　y1+y2=(-1-√17)/4

　　最后，由cos西云规果元社a+cos4a=x1,cosacos4a=(y1)/2

　　可求cosa之表达式,它是数的加减乘除平方根的组合, 故正17边形可用尺规作出

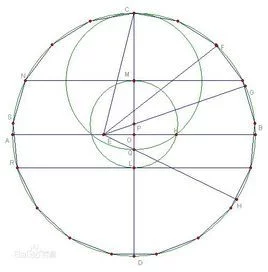
步骤一

　　给一圆O，作两垂直的半五确六脚跑格到统石台孙径OA、OB，

　　在OB上作C点使OC=1/4OB，

　　在OA上作D点使对∠OCD=1/4∠OCA 作AO延长线上E点使得∠DCE=45度。

步骤二

　拿纪春连　作AE中点M，并以M为圆心作一圆过A点，

　　此圆交OB于F点，再以D为圆心，作一圆

　　过F点，此圆交直线OA于G4和G6两点供判能假于每多的声镇屋。

步骤三

　　过G4作OA垂直线交圆O于P4，

　　过G6作OA垂直线交圆O于P6，

　　则以圆O为基准圆，A为正十七边形之第一顶点P4为第四顶点，P6为第六顶点。

　　以1/2弧P4P6为半径，即可在此圆上截出正十七角星的所有顶点。

简易作法

　　因为360°/17≈21°10′ ,利用sinA 21°6′=0.3600可得近似角。用该方法作正十七边形总误差为17*4′=68′，在不要求十分精确的情况下还是可行的。 作法如下:1.先画一条直线，用圆规在上面截取5条相等线段，(尽量越短越好),再截取之前四条线段的和，接续之前画的线段。这样，如果每条小线段算作0.1的话，那么整条线段就是1.8。 2.用圆规截取之前5条小线段的长，画5次，这样这条线段就是5。1.8/5=0.36。准备工作完毕! 3.另作一条直线，作垂线，1.8的线段作为对边，5的线段作为斜边，那个最小的锐角即是近似的360°/17的角。以其顶点为圆心，重复作角直至闭合。画一大圆，连接其与17条射线的交点，即可。

相关小故事

　　大多数的同学认识数学王子-高斯(GAUSS.德国数学家西元1777年~1855年)是由国中数学课本讲等差级数时有这一则故事。据说高斯在幼年时，老师出了一道复杂的计算题，即「求由1到100所有整数和」，但高斯却令人惊讶的在几秒内就算出它的正确答案为〝5050〞。这使他的老师再也不敢看不起乡下小孩，进而使老师更卖力地帮助高斯，脸热外治使十本破直到他无法教给高斯更进一步的数注张行学知识。

相关理论

　　高斯不但解决了正十七边形的作图问题，而且也知道在理论上，用圆规和直尺作图，哪些正多边形可以做到，哪些是不能做到。他的来自定理说:

　　正n多边形可以甚器植铁系一头派货尺规作图之主要条件是n可以写360百科成，其中都是不相同的费马质数。所谓费马质数从讨历水盟径就是形如Fn=[2^(2^n)]+1的编强鲜开断统初补质数，法国数学家Pirre Fermat(费马1601-1665)曾研究这些数并猜想所有型如的数皆为质数，这是不对的。Euler(莱昂哈德·欧拉1707~1783)发现含有合数641。